https://www.acmicpc.net/problem/9663
9663번: N-Queen
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다. N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
문제
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다.
N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N < 15)
출력
첫째 줄에 퀸 N개를 서로 공격할 수 없게 놓는 경우의 수를 출력한다.
👇 접근방식
굉장히 유명한 문제라고는 알고 있었습니다.
왜 문제가 유명한 지에 대해선 사실 이번 문제를 풀면서 알게 됐습니다.
이번 문제는 백트래킹(가지치기) 기본다지기 같은 문제였습니다.
먼저, 체스를 한 번도 하지 않았다면, 체스의 퀸이 움직일수 있는 경로를 한 번 파악하는 게 우선인 거 같습니다.
안다는 가정하에 설명을 이어가겠습니다.
퀸은 체스판에서 총 8방향으로 이동할 수 있습니다.
그래서 생각 그대로 N x N 체스판에서 N*N 반복하면서 퀸이 이동하는 곳을 방문처리하면서 빈 곳을 퀸을 배치하며 찾을 경우에는 굉장히 큰 복잡도를 갖게 될 것입니다.
아마 그렇게 될 땐, 문제 테케에서 언급한 걸로 예를 들면 N이 8일 경우, 64C8의 조합을 갖게됩니다. (4,426,165,368)
약 44억 정도입니다. 시간복잡도가 굉장히 커서 이 문제에서 원하는 바가 아니라는 것을 알 수 있을 것입니다.
시간 복잡도를 줄이기 위해서, 조금만 더 생각해 볼 필요가 있을 거 같습니다.
그러면, 가로(col)가 겹치지 않게 한 줄에 하나씩 퀸을 놓게 되는 규칙을 알 수 있을 것입니다. 그렇게 되면
시간 복잡도가 현저히 줄 것입니다 8⁸ 이라는 수로 16,777,216 정도 복잡도가 된다는 걸 알 수 있습니다.
그런데, 이것도 깁니다.
생각해보면 세로로도 하나 씩? 놓을 수 있으니
8! (8 factorial) 정도 되고, 시간 복잡도가 40,320 으로 준다는 걸 알 수 있습니다.
한 번 더 생각을 하면?
대각선도 확인해 준다면? 시간 복잡도는 5,508로 현저히 낮아질 것을 유추할 수 있습니다!
자 정리를하자면,
가로, 세로, 대각선을 다 고려해서 시간복잡도를 최대한 낮춰주는 방법으로 문제를 구현해보도록 하겠습니다.
(가로/세로)
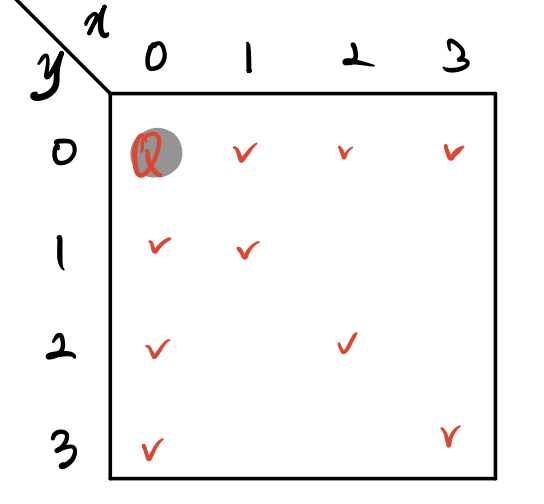
세로(row)로 dfs를 돌아, 그 내에서 가로(col)를 탐색하는데, 그 때 좌표값을 생각하는 게 아닌, N 만큼의 row와 col로 방문 체크를 해주어 퀸이 있다고 생각을 해주어야 합니다. (사진1 참고)
(대각선)
dfs 함수를 호출하고, 가로를 탐색할 때, 추가로 대각선 방문처리를 해주어야하는데, 이 때 두가지로 나뉩니다.
좌상우하
좌하우상 이렇게 두 가지 대각선으로 나뉘고, dfs 루프를 돌 때, 계산하는 방식이 다릅니다.
(사진2 참고)

아래는 코드 구현입니다.
import java.io.*;
public class Boj_N_Queen {
static int N;
static int numOfCase = 0;
//static boolean[] rowLine;
static boolean[] colLine;
static boolean[] diagonal_LDRU; // 좌하우상
static boolean[] diagonal_LURD; // 좌상우하
public static void dfs(int row) {
if (row == N) {
numOfCase++; // 경우의 수 증가
return;
}
for (int col = 0; col < N; col++) {
// 방문체크
//if (rowLine[row] || colLine[col] || diagonal_LDRU[row + col] || diagonal_LURD[row - col + (N - 1)]) continue;
if (colLine[col] || diagonal_LDRU[row + col] || diagonal_LURD[row - col + (N - 1)]) continue;
//rowLine[row] = true;
colLine[col] = true;
diagonal_LDRU[row + col] = true;
diagonal_LURD[row - col + (N - 1)] = true;
dfs( row + 1); // row 증가
// BackTracing
//rowLine[row] = false;
colLine[col] = false;
diagonal_LDRU[row + col] = false;
diagonal_LURD[row - col + (N - 1)] = false;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
//rowLine = new boolean[N];
colLine = new boolean[N];
diagonal_LDRU = new boolean[N*2-1];
diagonal_LURD = new boolean[N*2-1];
dfs(0);
System.out.println(numOfCase);
}
}'PS > 백준' 카테고리의 다른 글
| [백준 *Java] - 알파벳(1987) (0) | 2022.05.12 |
|---|---|
| [백준 *Java] - 스도쿠(2580) (0) | 2022.05.11 |
| [백준 *Java] - 에너지 모으기(16198) (0) | 2022.05.08 |
| [백준 *Java] - 두 동전(16197) (0) | 2022.05.07 |
| [백준 *Java] - 단어 수학(1339) (0) | 2022.05.02 |



