산술 오버플로 란?
컴퓨터는 수학자들이 만든 기계들이며 수학에 따라 움직입니다만, 현실 세계에 존재하는 물건인지라 엄연한 제한이 있습니다.
그 중 가장 대표적인 제한이 바로 유한성입니다.
수학에는 어떤 변수 n이 있다고 하면 이 변수에 담을 수 있는 숫자에는 제한이 없습니다.
그러나
컴퓨터의 모든 변수에는 담을 수 있는 크기가 제한되어 있습니다.
따라서, 수학적/논리적으로는 완전히 정당한 알고리즘도 프로그램으로 구현했을 때,
예상과 다르게 동작하는 경우를 흔하게 볼수 있습니다.
이 문제를 일으키는 흔한 원인이 바로 산술 오버플로 (Arithmetic overflow) 입니다.
어떤 식의 계산 값이 반환되는 자료형의 표현 가능한 범위를 벗어나는 경우를 말합니다.
현대 많은 언어들에서는 메모리가 허락하는 한도 내에서 가능한 한 큰 정수를 구현하는 클래스들을 표준 라이브러리에서 제공하기 때문에 산술 오버플로를 신경 쓸 일이 크게 줄어들었습니다.
그러나,
이런 클래스들은 훨씬 많은 메모리와 시간을 필요로 하기 때문에 여전히 공부할 가치는 충분합니다.
너무 큰 결과
우리가 흔히 사용하는 32비트 자료형의 범위를 넘어가면 64비트 정수를 사용하거나?
큰 정수 구현을 이용해야 합니다.
하지만,
습관적으로 32비트 정수를 쓰는 실수가 꽤나 흔히 발생합니다.
그 외에도 최종 결과는 64비트 정수를 이용하면서 중간 계산 값을 32비트 정수로 전달하는 실수를 자주 볼 수 있습니다.
너무 큰 중간 값
산술 오버플로가 문제가 되는 또 다른 대표적인 경우는 프로그램의 출력 값의 범위는 작지만,
중간 과정에서 큰 값을 일시적으로 계산해야 하는 경우입니다.
Ex. 두 개의 32비트 부호 있는 정수를 받아 이 둘의 최소공배수를 반환하는 함수를 생각해 봅니다.
아래의 코드는 의사코드입니다.
lcm (50000,10000)을 계산해봅니다.
사실 최소공배수까지 갈 것도 없이 50000 * 2 = 100000 이기 때문에, 이 함수의 반환 값은 그냥 100000 이 되어야 할겁니다.
입력과 출력이 모두 32비트 정수 안에 충분히 들어가기 때문에 산술 오버플로의 여지는 보이지 않습니다.
그런데,
실제로 이 값을 계산해 보면 엉뚱한 값이 나옵니다.
대체 왜 이런일이 발생할까요?
문제는 계산의 중간 값이 32비트 정수 범위를 넘어간다는 데 있습니다.
이 경우, a * b 의 값은 5 * 10⁹ 이 되는데, 이 값은 부호 있는 32비트 정수형의 최대치인 2,147,483,647 을 가뿐히 넘깁니다.
이 때, 우리(개발자)에게 아무 경고도 하지 않고 이 값의 마지막 32비트만을 취해서 값을 반환합니다.
즉, 자료형의 표현범위가 넘어가면 우리가 원하는 답이 담기지 않습니다.

int gcd(int a, int b); // 두 수의 최대공약수를 반환.
int lcm(int a, int b) { // Ex) a = 50,000 / b = 100,000
return (a * b) / gcd (a, b);
}
너무 큰 '무한대' 값
알고리즘 문제를 풀다가, 실제로 나타날 리 없는 매우 큰 값을 반환하는 경우가 있습니다.
이러한 경우, 값들이 서로 더해지거나 곱해지는 경우가 없는 지 잘 살펴보고 이럴 때,
오버플로가 나지 않을 크기의 값을 선택하는 것이 좋습니다.
오버플로 피해가기
오버플로가 발생한다는 사실을 알았을 때, 어떻게 코드를 고치면 오버플로를 막을 수 있을까요?
첫 번째 방법
더 큰 자료형을 쓰는 것입니다.
위에 예시로 둔 최소공배수 lcm()은 64비트 정수형을 사용하면 쉽게 저장할 수 있습니다.
* 첫 번째 방법
int lcm(int a, int b) { // int 의 최대 값은 2,147,483,647 입니다.
return (a * (long)b) / gcd(a, b); // long으로 형변환
}
위 와같이 자동형변환이 가능합니다.
자료형의 프로모션이라고 하며
JAVA 에서는 Widening conversion 라고 불리웁니다.
크기가 더 작은 자료형을 더 큰 자료형에 대입할 때, 자동으로 작은 자료형이 큰 자료형으로 변환되는 현상을 뜻합니다.
참고 링크
https://www.geeksforgeeks.org/type-conversion-java-examples/두 번째 방법
오버플로가 나지 않도록 연산의 순서를 바꾸는 것입니다.
gcd(a, b) 는 a 와 b 모두의 약수이니만큼, a 와 b 를 곱하기 전에, 미리 gcd(a, b)로 나누어 버려도 나누어 떨어집니다.
그래서 곱셈을 하기 전에 미리 한 쪽을 gcd로 나누어 버리면 됩니다.
* 두 번째 방법
int lcm(int a, int b) {
return a * (b / gcd(a, b));
}그러면 먼저 100000 / 50000 가 계산되어 2가 나와, 여기서에서 2 * 50000 를 하기 때문에 어떤 오버플로도 없이 안정적으로 100000을 구할 수 있게됩니다.
두 번째 방법 - (2)
문제에 따라 계산 방법을 다르게 해, 오버플로를 피해가는 방법입니다.
이항 계수를 계산하는 경우가 그 좋은 예입니다.
이항 계수를 가지고 계산한다고 하면,
n이 30/ r이 15 일 때, 값은 155,117,520 으로 최종 결과 값이 32비트 정수에도 쉽게 저장할 수 있습니다.
그러나 이 식을 계산하려고 할 때, n! 부분을 계산할수 없다는 게 문제입니다.
30!은 너무 큰 수라, 64비트 정수의 표현 범위도 훌쩍 넘어버리기 때문입니다.
따라서,
이런 방식으로 이항 계수를 계산하려고 하면 큰 정수 구현을 이용하지 않으면 안됩니다.
그러나,
이항 계수에 대한 성립하는 다음과 같은 점화식을 이용하면 오버플로에 신경 쓰지 않고 구할 수 있습니다.
아래의 공식에 파스칼의 법칙이 있습니다.
이 점화식을 이용한 이항 계수의 계산에서 중간 값은 항상 최종 결과와 같거나 더 작으므로,
32비트 정수형만을 가지고 계산할 수 있습니다.


세 번째 방법(Java)
오버플로를 검사하는 간단한 방법을 만들어 실제로 작업을 수행하고 결과가 소스 유형의 범위 내에 있는 지를 확인을 하는것입니다.
public int addWithOverflowCheck(int a, int b) {
long result = ((long) a) + b;
if (result > Integer.MAX_VALUE) {
throw new RuntimeException("Overflow occured");
} else if (result < Integer.MIN_VALUE) {
throw new RuntimeException("Underflow occured");
}
return (int) result;
}
// https://wiki.sei.cmu.edu/confluence/
카네기멜론 대학교 소프트엔지니어링 학회 사이트세 번째 방법 - (2)
더 큰 값을 허용하지 않거나 오버플로가 발생하는 것을 원하지 않고 대신 예외를 던지고 싶은 상황이라면?
Java 8부터 사용할 수 있는 메소드입니다.
int value = Integer.MAX_VALUE-1;
for(int i = 0; i < 4; i++) {
System.out.println(value);
value = Math.addExact(value, 1);
}
//정적 메서드 addExact() 는 일방적인 추가를 수행하지만,
//작업 결과 오버플로 또는 언더 플로가 발생하면 예외가 발생합니다.
출력 값
2147483646
2147483647
Exception in thread "main" java.lang.ArithmeticException: integer overflow
at java.lang.Math.addExact(Math.java:790)
at Main.main(Main.java:6)
Process finished with exit code 1
참고 : https://memo-the-day.tistory.com/121네 번째 방법(Java)은
Java 내에 있는 API 를 사용하는 겁니다. 큰 수를 담을 수 있는 BigInteger 를 사용합니다.
BigInteger 는 오버플로를 하지 않습니다. 필요한 경우 사용 가능한 모든 메모리를 사용합니다.
BigInteger 값 범위는 JVM에서 사용 가능한 메모리 양을 제외하고는 제한되지 않습니다.
BigInteger largeValue = new BigInteger(Integer.MAX_VALUE + "");
for(int i = 0; i < 4; i++) {
System.out.println(largeValue);
largeValue = largeValue.add(BigInteger.ONE);
}
출력 값
2147483647
2147483648
2147483649
2147483650https://docs.oracle.com/javase/8/docs/api/java/math/BigInteger.html
BigInteger (Java Platform SE 8 )
Immutable arbitrary-precision integers. All operations behave as if BigIntegers were represented in two's-complement notation (like Java's primitive integer types). BigInteger provides analogues to all of Java's primitive integer operators, and all relevan
docs.oracle.com
추가로, 오버플로에 대해서 각 연산별로 되는지 안되는지 나타내는 그림입니다.
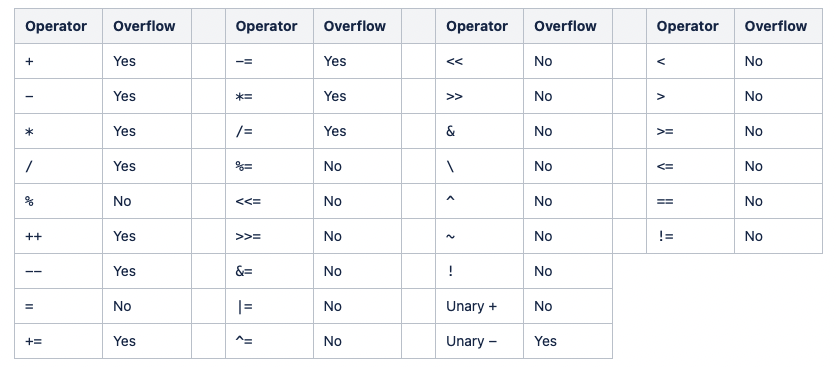
최종적으로 정리해서 말을 하자면
오버 플로우 대처 방법은
예외처리를 던져주던지,
업캐스팅을 하던지,
산술을 쪼개 계산을하던지,
BigInteger 를 사용하는 방법이 있습니다.
'CS > Other' 카테고리의 다른 글
| [git] - Git push 오류 해결방법(Updates were rejected because the tip of your current branch is behind) 단 주의해야합니다. (0) | 2022.06.10 |
|---|---|
| TDD란? (0) | 2022.04.30 |
| Git과 Github에 대해서... (0) | 2022.04.03 |
| 공간복잡도(Space Complexity) 란? (0) | 2022.03.11 |
| 시간복잡도(Time Complexity) 란? (0) | 2022.03.08 |
