2263번: 트리의 순회
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
www.acmicpc.net
문제
n개의 정점을 갖는 이진 트리의 정점에 1부터 n까지의 번호가 중복 없이 매겨져 있다. 이와 같은 이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n(1 ≤ n ≤ 100,000)이 주어진다. 다음 줄에는 인오더를 나타내는 n개의 자연수가 주어지고, 그 다음 줄에는 같은 식으로 포스트오더가 주어진다.
출력
첫째 줄에 프리오더를 출력한다.
접근 방식
이 문제에서 중요한 부분을 2 가지로 나눌 수 있을 거 같습니다.
- 분할 정복이 어떤 부분에서 사용이 되는 지?
- 재귀적으로 코드 구현을 어떻게 할 것인 지?
분할 정복은 어디서 사용될까요?
문제에서 언급한 건, postorder(후위) 와 Inorder(중위) 를 이용하여, preorder(전위) 를 구할 수 있다고 했습니다.
즉, 후위와 중위 flow를 그려보면서 전위를 어떤식으로 찾을 지 알아 차리시면, 분할 정복이 왜 사용되는 지 이해가 되실겁니다.
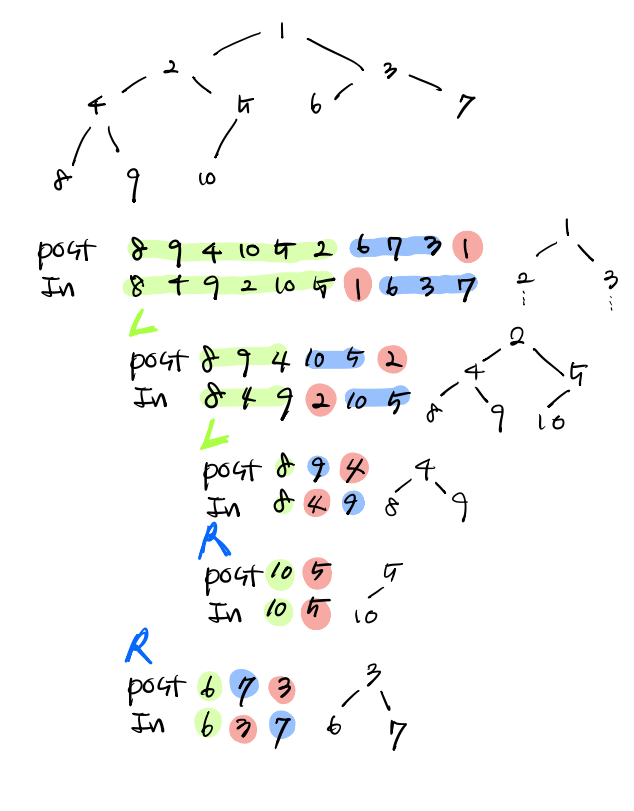
위 그림1 을 보고 설명을 해드리겠습니다.
트리를 임의로 1~10 까지 숫자로 그려놓고, 중위와 후위를 미리 값을 구한 뒤에 전위를 어떤식으로 구하면 될지 그려놓은 그림입니다.
여기서 핵심은
후위(post)는 부모 node(또는 root) 를 나타내고,
중위(in)는 left, right 를 찾을 수 있다.
그리고, 후위의 맨 끝은 무조건 부모 node(또는 root)
입니다.
그리고 그림에서 연두색은 왼쪽, 파란색은 오른쪽, 빨간색은 부모node를 의미합니다.
Flow
- 후위(post) 맨 끝 값인 node를 부모 node로 생각하기
- 후위(post)에서 부모 node를 찾았다면, 그 부모 node로 중위(in)에서 pivot 역할 하듯 반으로 나눔.
- 중위(in) 에 왼쪽은 부모 node 기준으로 왼쪽에 있는 트리이고, 오른쪽은 부모 node 기준으로 오른쪽에 있는 트리입니다.
- 이 과정을 분할정복으로 나눠서 생각하고 계산해야한다고 생각하기.
위 과정을 어느정도 설명했다고 해서, 이 문제를 풀 수 있는 건 아니였습니다.
분할 정복을 이용해서 결국은 preorder 를 구해야하는 문제이니깐요.
이 부분은 코드를 보면서 설명드리겠습니다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int[] inorder, inIdx, postorder;
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int n = Integer.parseInt(br.readLine());
inorder = new int[n + 1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++)
inorder[i] = Integer.parseInt(st.nextToken());
postorder = new int[n + 1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++)
postorder[i] = Integer.parseInt(st.nextToken());
// * inorder 인덱스
inIdx = new int[n + 1];
for (int i = 1; i <= n; i++)
inIdx[inorder[i]] = i;
solve(1, n, 1, n);
System.out.println(sb.toString());
}
static void solve(int inorderStart, int inorderEnd, int postStart, int postEnd) {
// 탈출 조건 (idx 위치가 start 가 end 보다 클 경우)
if (inorderEnd < inorderStart || postEnd < postStart) {
return;
}
int root = postorder[postEnd];
int rIdx = inIdx[root]; // * inIndx 배열을 사용하는 이유
sb.append(root + " ");
// 분할 정복
int len = rIdx - inorderStart;
solve(inorderStart, rIdx - 1, postStart, postStart + len - 1);
solve(rIdx + 1, inorderEnd, postStart + len, postEnd - 1);
}
}
위 코드는 아래와 같은 Flow 로 preorder 가 만들어 집니다.


위에서 코드에서 사용한 inIdx 배열을 사용하는 이유를 잘 분석해서 보시는 게 좋습니다.
'PS > 백준' 카테고리의 다른 글
| [백준 *Java] - 하노이 탑 이동 순서(11729) (0) | 2022.06.09 |
|---|---|
| [백준 *Java] - 4연산(14395) (0) | 2022.06.03 |
| [백준 *Java] - 2048(Easy)(12100) (0) | 2022.05.16 |
| [백준 *Java] - 구슬 탈출 2(13460) (0) | 2022.05.15 |
| [백준 *Java] - 가르침(1062) (0) | 2022.05.15 |



